In our last article we looked at how to use Sumstix and number bonds to teach your child to add and subtract single digit numbers . These tools work brilliantly for totals up to ten, and those facts are non-negotiable to make sense of higher level maths, like fractions and algebra. But what happens when the total is greater than ten?
Addition strategies for totals over ten
While it will serve your child well to memorise these facts, they can get away with using strategy to calculate them as long as the strategy is quick and easy to implement. We need to keep cognitive load low when working on more complex problems. Here are two of our favourite strategies for adding ‘big’ single digit numbers:
- Make ten: when adding 9 or 8 to ten, it’s easy to ‘pinch’ or borrow 1 or 2 from the other number to complete a ten and make the answer to the problem obvious. Here’s how we illustrate the idea using Sumstix:
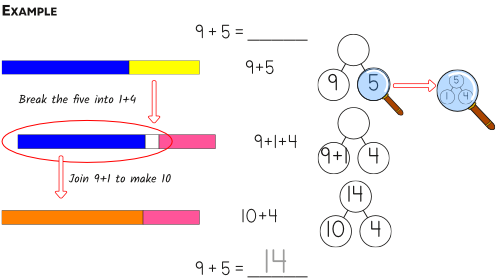
- Double plus one: For some reason, most people find learning the doubles (like 5 + 5 or 8 + 8) easier than learning the other single digit addition facts. The ‘double plus one’ strategy leverages this knowledge by recognising that sums like 5 + 6 or 7 + 8 are just one more (or one less) than a double.
The subtraction “shopping” trick
When it comes to subtraction, we have one favourite strategy that is a game changer for most kids. I like to present it with a little “role play” story: (We’ll use the subtraction 14 – 8 for the example)
Imagine you’re at the shop and have a ten dollar note in one pocket and four dollars worth of coins in the other. You want to buy something that costs eight dollars.
Which pocket to do you reach into? The one with ten dollars, right? You hand the person at the checkout the ten dollars and they give you how much change?
Yes, two dollars. Then you put the two dollar coin in the pocket that already has four dollars worth of coins in it. So, how much money is in your pocket now? Of course, it’s six!
That story is always a major light bulb moment for students! It makes higher order subtractions super easy.
Multi-digit addition algorithm
Now we can extend those basic ideas to adding and subtracting larger (multidigit) numbers but, at the lower levels, it is much less confusing, and more conducive to developing good number sense, to teach the child basic addition and subtraction algorithms. That way, the child can get lots of practice using these basic strategies on single digit numbers before extending the idea.
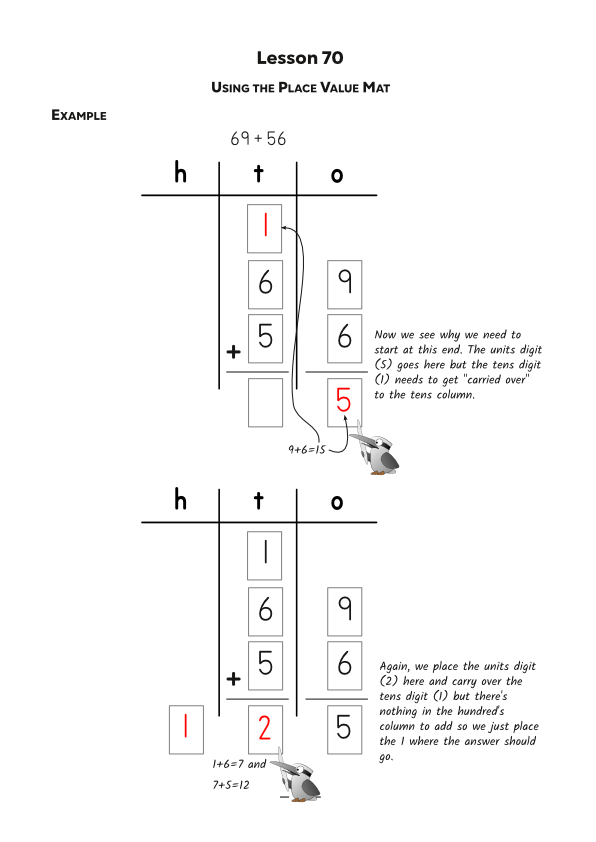
The addition algorithm is fairly straightforward and universally accepted. We just write the numbers to be added under each other, making sure we line up the place values, then add down each column working from right to left.
In Milestone Maths we introduce this idea over several lessons, beginning with hands on practice using number cards then moving to a place value chart and finally on a simple grid. For those who need a quick refresher of this algorithm, here’s an example calculation using a place value chart and number cards:
The Great Controversy: Subtraction Algorithms
Now for some controversy. When it comes to subtraction there are two algorithms that fight for supremacy in the classroom. One was almost universally taught in Australia for decades until the nineteen-nineties when another “new and better” way was introduced. I’ve lost count of how many parents have complained to me that they can’t understand the way their kids were taught to subtract but their teacher insisted that there was only one right way to do subtraction.
But the shocking truth is that both algorithms are ancient and neither is truly superior to the other. I have a slight preference for the “old” method because I like it’s consistency and it’s very similar to the algorithm used inside the ‘brain’ of a computer but when I’m tutoring I teach both methods and tell the student to stick with the method that they find easier to understand. We do exactly the same in Milestone Maths:

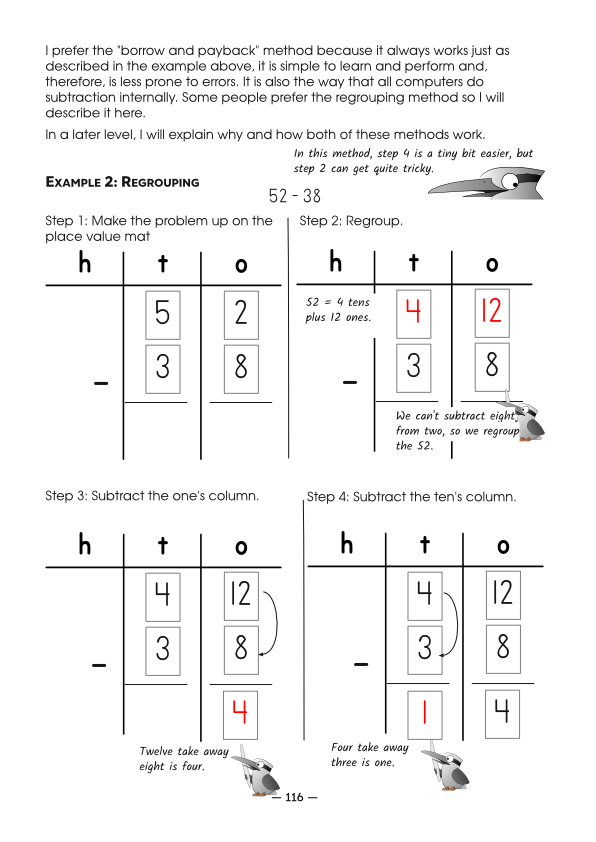
The “borrow and payback” (or equal adding) method is the “old way” and the “regrouping” method is the “new way.” It really doesn’t matter which algorithm you (or your child) use, so long as you do it consistently and get the correct answer.
In Milestone Maths we give copious practice with these algorithms because they lay an important foundation for number sense and algorithmic thinking which smooths higher level maths. They are also another way to practice the all important maths facts.
So which subtraction algorithm do you like and why? Let us know in the comments!


